リンゴとカキの観察 その2(花や果実・葉のつき方など・・・数学的な側面から)
 |
「『よく見る』とは上から見たり,下から,横からといろいろ見ることだね。それにあれこれといじくり回してもいいよ。すきなように観察(かんさつ)しようよ。それで,何か気がついたことがあるかな。」 |
 |
「うーん,どちらもおいしそうね。いや,観察するんだった。わたし,食べたくなっちゃうな。食べたいのはがまんしてよーく観察しなくちゃ。」 |
 |
「あれ! 花ちゃん。両方を上から見て気がついたんだけど,リンゴは五角形だけど,カキは四角形だぞ。中はどうなってるかな。たてや横に切ってみよう。」 |
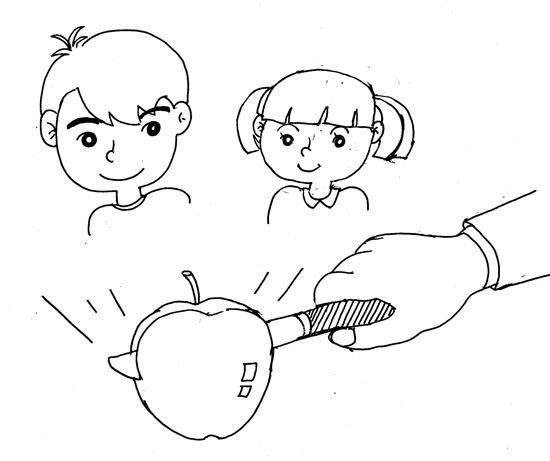 |
|
 |
「あれ! たてに切ったのでは分からなかったけど,リンゴを横に切ると,リンゴには5つの部屋みたいのがあって星の形にならんでいるわ。でも,カキは8つの部屋だ。8は4の2倍だから,あれ!」 |
 |
|
 |
|
 |
「カキにはへたがあるだろう。いくつあるか数えてごらん。」 |
 |
「へたは4つ。ということは……。」 |
 |
「二人とも気がついたみたいだね。カキは4の数がもとになっているだろう。ところが,リンゴは5の数がもとになっている。これはね,花びらの数にも関係(かんけい)しているんだよ。カキを4数性(すうせい)の花。リンゴを5数性の花というのさ。ユリなどは3の数がもとになっているから,果実の形は三角形なんだ。なんだか,規則(きそく)があるみたいだね。」 |
花や果実の構造・葉のつき方について……数学的な側面からの一考察
リンゴは5の倍数,カキは4の倍数,ユリは3の倍数になっていることなど,数学的に考えていくことは楽しいことです。花や果実に限らず,葉のつき方,枝の出方なども決してでたらめではなく,すべてがある規則に従っているのです。植物をぼんやりと見ていたのでは分かりません。私たちが花が美しいとかいうのは,色や形のほかに花びらやその他植物の構成要素の数学的な規則正しい配列の仕方なども関係しているのです。 例えば,ヒメムカシヨモギという帰化植物がありますが,直立した茎に無数の葉をつけます。ちょっと見た目ではでたらめに見えますが,一定の法則があります。どういうことかというと,葉の出る位置が135度ずつ回転しながらついています。135度は360度の8分の3ずつ回っているということです。つまり,どの葉からでも結構ですが,数え始めて8枚目の葉でちょうど3周まわって元の位置につくということです。 どんな植物でも葉の位置をずらしながら伸びていき,このずれ方を植物学的用語では「葉序」といい,どのようにずれるかは,植物の種類によって定まっています。まず360度の2分の1ずつのものがあります。1/2の次に1/3,2/5,3/8,5/13……という数列になり,これは数学的には「フィナボッチ数列」と呼ばれ,植物の葉序がこの数列に従っていることを「シンパー・ブラウンの法則」と呼ばれています。 植物がどこでこのような高等数学を学んだのかは分かりませんが,植物たちはほとんどがこの法則に従って成長しているのです。そして,この葉序の配列を続けていくと,不思議なことに最も美しいと言われる黄金比の逆数に近づいていくという結果になります。 しかし,このことは,植物が数学的な法則に従っているということではありません。数学がもともと自然界にある存在する法則を解き明かしただけなのです。自然の摂理の偉大さ,不思議さ,深遠さなどなど,さまざまに思い感じる今日このごろです。
